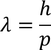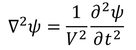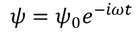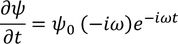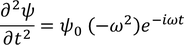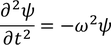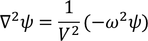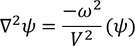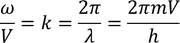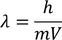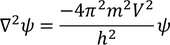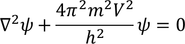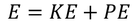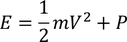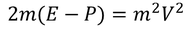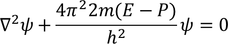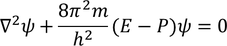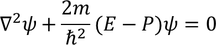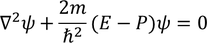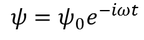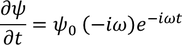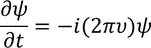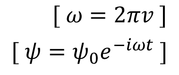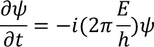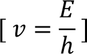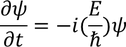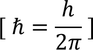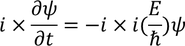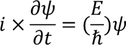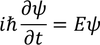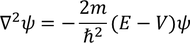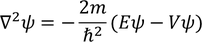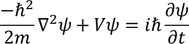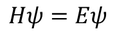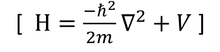Schrodinger time independent equation:
Let us consider an electron of mass 'm' moving with velocity 'V'. As the electron is spreading like a wave, its wave length is given by
Let the differential equation for probability of electron is given by
Solution for the above differential equation is
by partially differentiating with respect to time on both the sides, we get
by re-differentiating, we get
by substituting Eq - (2) we get,
by substituting the above equation in Eq - (1) we get,
Now let us consider
Now substituting the above value in equation 3 we get,
We know that the total energy is the sum of kinetic energy and potential energy
Substituting this equation in equation - (4)
As time is not involved in this equation, it is known as Schrodinger time independent equation.
Schrodinger time dependent equation
By eliminating the energy term E from this we get Schrodinger time dependent equation. We know that the solution for the differential equation is
Partially differentiating with respect to time 't' on both the sides we get,
Schrodinger time independent equation is,
This equation can be written as,