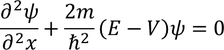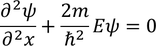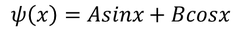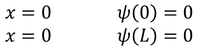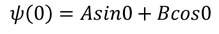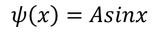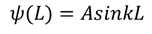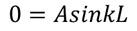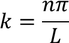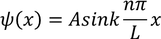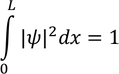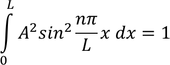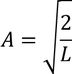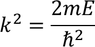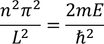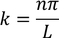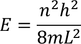Particle in a rigid one dimensional infinite potential well
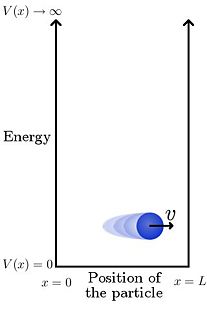
Let us consider an electron of mass 'm' is restricted in a one dimensional infinite potential well, whose boundaries are x=0 to x=L.. Electron can move freely with in the well, where the potential energy is zero that is it is on the boundary then,
Let us consider Schrodinger time independent equation (one dimensional)
Solution for the above differential equation
Applying the limits in one dimensional direction, that is x=0 and x=L we get,
After applying the first boundary condition to Eq - (1) we get,
Applying the second boundary conditions that is x=L to Eq -(2), we get
By using normalized equation, along x-axis in between the limits of x 0 to L we get,
On integrating this equation, we get the constant 'A'
The general wave function is
'E' is the energy of the electron in that infinite potential well.