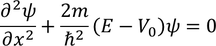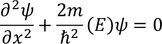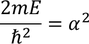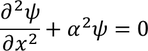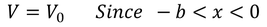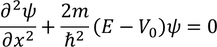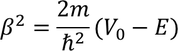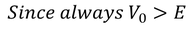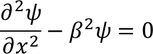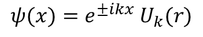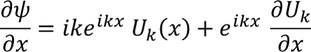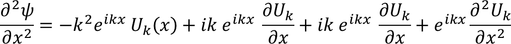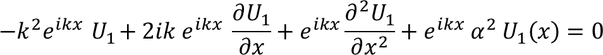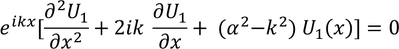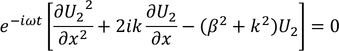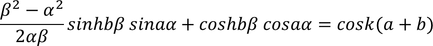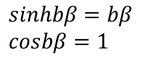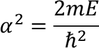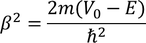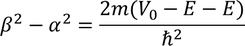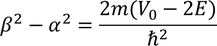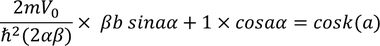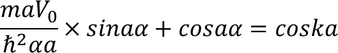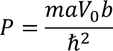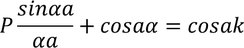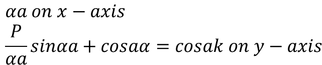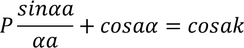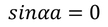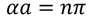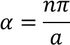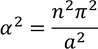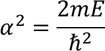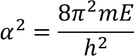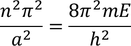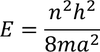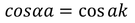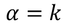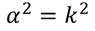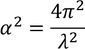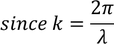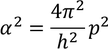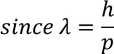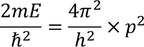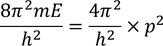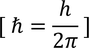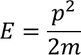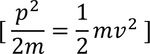Kronig Penney model
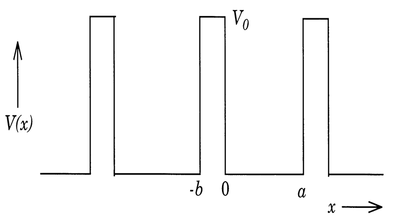
- The essential behaviour of electron may be studied by periodic rectangular well in one dimensional which was first discussed by Kronig Penney in 1931.
- It is assumed that when an electron is near the positive ion site, potential energy is taken as zero. Where as outside the well, that is in between two positive ions potential energy is assumed to be Vo.
The wave function associated with electron when it is in first state is derived as follows
Let us consider
Then the equation transforms to
The wave function associated with the electron when it is in second state is derived as follows. Here the conditions are
Let us consider
Hence the equation transforms as
Bloch has given the solution for Schrodinger equation as
Partially differentiating the above equation, we get
Again differentiating we get,
By substituting this value is equations 1 we get,
Similarly by substituting this in equation 2
By writing the general solutions for equations 3 and 4 we get four constants A,B,C,D. To know the values of these constants we apply the boundary conditions, as x=0, x=a, x=-b. In evaluation the constants A,B,C,D are vanished and the final equation obtained is
This equation can not describe motion of electron with periodic motion. In order to express the relation in more simplified form.
So let us consider Vo tends to infinity then, b=0 and
So let us consider Vo tends to infinity then, b=0 and
Then the initial conditions of the constants α^2 and β^2
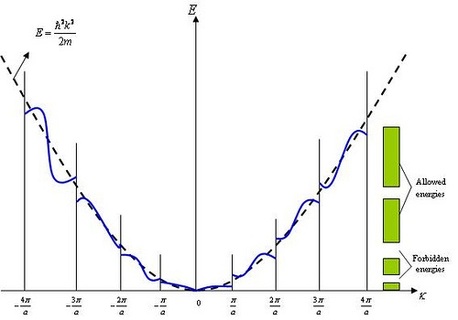
Conclusions from graph:
1. The substance contains a number of allowed and forbidden energy gaps.
2. Width of the allowed band increase with increase of αa.
1. The substance contains a number of allowed and forbidden energy gaps.
2. Width of the allowed band increase with increase of αa.
then
We also know that
Equating both the above equations we get,
This expression shows the behaviour of the electrons supports quantum free electron theory
then
We know that
Equating both the equations we get,
after a simple calculation, we get
This expression shows all the electrons are free to move without any constrains. This supports classical free electron theory.
Brillouin zones
|