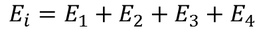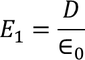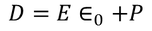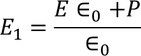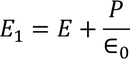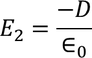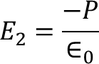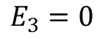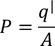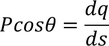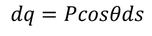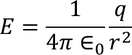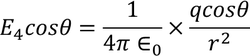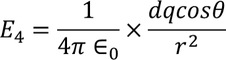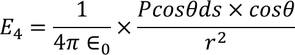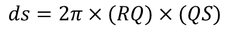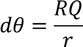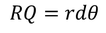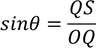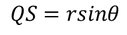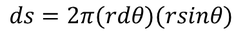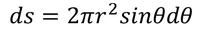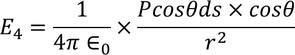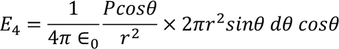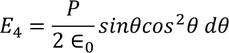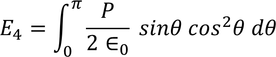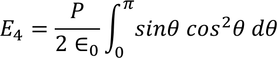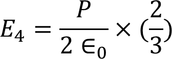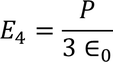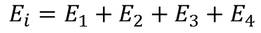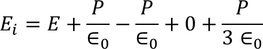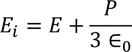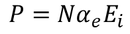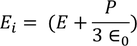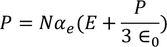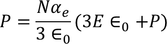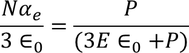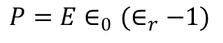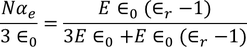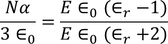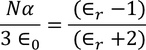Internal field or Local field in solids
Consider a dielectric material and is subjected to external field of intensity E1. The charges are induced on the dielectric plate and the induced electric field intensity is taken as E2. Let E3 be the field at the center of the material. E4 be the induced field due to the charges on the the spherical cavity. The total internal field of the material is
Now consider the Electric field intensity applied E1
Substituting the Electric flux density D in E1, we get
E2 is the Electric field intensity due to induced or polarized charges
Here the charge is induced due to the induced field so the the electric flux density D changes to the electric polarization P
Since we have considered that the specimen is non polar dielectric material, at the center of the specimen the dipole moment is zero and hence the electric field intensity at the center is zero due to symmetric structure.
Now consider a circle from the center of the dielectric material. In order to calculate the electric field intensity E4 on the surface of spherical cavity, the polarization should be calculated by resolving it into two components, as shown in the following figure.
As we know the polarization P is the induced charge per unit area
Here the polarization changes to its component we have divide in the figure and the charge changes to dq where the area of cross section changes to ds
Now this equation can be solved by finding out the values of the charge dq in the surface are ds. We know the Electric field intensity E
Multiplying with the cosine angle on both the sides we get
Now by applying all the present condition for the above equation we
Now substituting the charge dq in the above equation we get
In the above equation ds should be calculated. Consider the spherical cavity and mark the points R and Q on the sphere of radius 'r' as shown in the above figure and drop vertical line from Q and mark it as S. By applying the surface area of a sphere formula we get,
Now consider the right angled triangle OQS from the figure
Now substituting the values RQ and QS in the surface area we get,
Now substituting all the values in the electric field intensity on the spherical cavity E4 we get,
Integrating with in the limits 0 to π
On solving the integration we get,
So the total electric field
Hence the Internal field obtained is
Clausius Mossotti's equation
It gives the relation between the dielectric constant and the ionic polarizability of atoms in dielectric material. If there are N number of atoms, the dipole moment per unit volume which is called Polarization is given by,
we know internal field
From above equations
we know polarization from the relation between polarization and dielectric constant
from the above two equations we get,