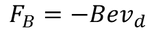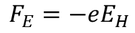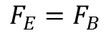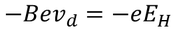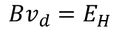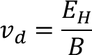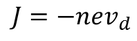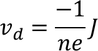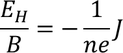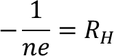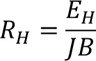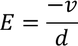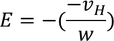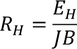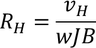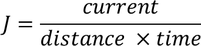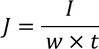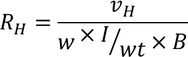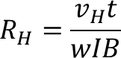Hall's Effect or Hall's law:
When a semiconducting material carrying current is placed in a transverse magnetic field, a potential is developed in the direction perpendicular to both current and the magnetic field. This phenomenon is called Hall effect. The produced voltage is called Hall voltage.
Consider a semiconducting slab carrying current 'I' along positive x-direction. A transverse magnetic field is applied along positive y-direction. According to Fleming's left hand rule, the electron will experience the force in upward direction. So, the electrons which are at the bottom of the metal, will drift towards the surface. This leads to the generation of current and voltage.
Consider a semiconducting slab carrying current 'I' along positive x-direction. A transverse magnetic field is applied along positive y-direction. According to Fleming's left hand rule, the electron will experience the force in upward direction. So, the electrons which are at the bottom of the metal, will drift towards the surface. This leads to the generation of current and voltage.
Force experienced by the electrons due to the magnetic field is given by
Force due to the applied electric field is given by F=E*q. Here it is transformed as
At equilibrium both the forces are equal so,
Equating both the above drift velocities we get
So, the Hall's coefficient is given by
Determination of Hall's coefficient in terms of Hall voltage:
We know by the definition of electric field is applied voltage per unit distance
By Hall's law we know
By simplifying both the above equations, we get,
By the definition of current density we have,
Substituting the Current density value in the above Hall coefficient equation, we get