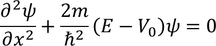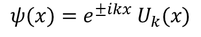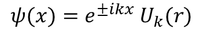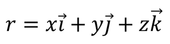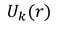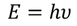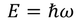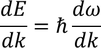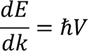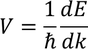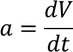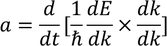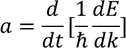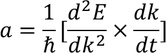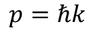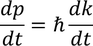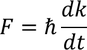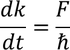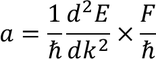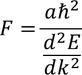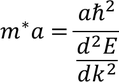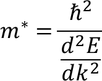Introduction:
- In classical free electron theory, conduction of electrons in a metal experiences zero potential.
- As per quantum free electron theory, conduction of electrons in a metal with constant potential, but
- According to band theory the potential experienced by an electron is perfectly periodic with the periodic lattice.
Bloch's theorem:
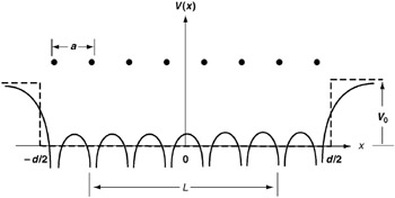
- When an electron is near the positive ion site, it's potential is minimum and when an electron is between the two positive ions, it's potential is maximum. i.e., potential of electrons also varies periodically.
- If 'a' is the inter atomic distance, the value of 'V' potential is same at all the points which are separated by the distance 'a' and this can be expressed mathematically [ V(x) = V(x+a) = V(x+2a). . . . . . . . . . . = V(x+na) ]
- By applying the periodic potential, Bloch has shown solution for one-dimensional Schrodinger wave equation,
Effective mass of an electron:Let us consider an electron of charge 'e' and mass 'm' moving inside a crystal lattice. When an external force is applied electron gets accelerated and the force created is F=m* a. Where m* is called effective mass of an electron.
Definition of m* : The mass of an electron when it is moving in crystal lattice with periodic potential under external force is called Effective mass (m*). The velocity of an an electron is taken as
Energy associated with the wave is given by
Differentiating on both the sides we get,
We know that acceleration is rate of change of velocity
Now let us consider the momentum
Differentiating on both the sides
We know that the rate of change of momentum 'p' is nothing but the force applied on that object 'F'
Substituting the above equation in equation 1 we get,
We know that F=m* a by the definition of effective mass of an electron. So by equating both the equations we get
m* varies with respect to nature of crystal and direction of motion of an electron. Its value may be larger or smaller than original mass 'm'.
|